ポートフォリオをExcelで作りたい!
証券アナリストの試験も終わり、久々にブログ書く時間ができました。
さて今回は、株式投資をしている人が一度は憧れる(?)、Excelで作る株式ポートフォリオの作成手順について紹介したいと思います。
実際にポートフォリオ作ってみた
今回はトヨタ自動車、ソニー、みずほ銀行への分散投資を行った際のポートフォリオをgoogleスプレッドシートにて作成しました。
以下が分散時のポートフォリオとなります。
このようにグラフにすると、個別銘柄だけではリスク7.14%が最低だったのが、分散投資を行うことで6.83%までリスクを下げることが分かりやすくなりますね。
さて作る手順ですが、まずは2009年10月〜1015年10月の5年間の月次時系列データ(マネックス証券より抽出)を元に、月次リターンとリスク、銘柄間の相関係数を算出しました。
これらと合わせ、投資配分(10%単位)を変数として、ポートフォリオの月次リターン/リスクがどのように変化するのかを表したのが上記グラフとなります。
以下の方法を覚えれば、銘柄数を増やしてもポートフォリオのリターン/リスクを計ることができるので、リンクも参照しながら是非実践して作ってみましょう。
それでは作成手順です。
リターンを求める
まずリターンの出し方です。
リターンは単純平均となるので、前月比騰落率の範囲を=averageで計算します。
図ではトヨタ自動車の過去5年間平均リターンを計算しています。(1.19%)
リスクを求める
次にリスクです。
株式投資におけるリスクとは、リターンがどれだけ大きく上振れ、下振れするか?です。
この計算については株価がランダムウォークし、正規分布に従うことを前提にするのが一般的です。
そのためリスク計算については、標準偏差という値を求めます。
標準偏差(standard deviation)(σ:シグマ)は関数=stdevで範囲を指定すれば、一発で出てきます。
※具体的には、{(個々のリターン)-(平均リターン)}^2を合算し、平方根を取ることで求められます。
図では、トヨタ自動車の標準偏差を求めています。(7.14%)
相関係数を求める
次に相関係数についてです。
相関係数(correlation)(ρ:ロー)とは、ある2つのデータがどの程度似通っているかを、数値で表したものです。
全く同じ傾向であれば1.0、完全に独立した動きであれば0、全く逆の傾向があれば-1.0という値を取ります。
Excelでは関数=correlで2つのデータ範囲を指定することで、求められます。
図では、トヨタ自動車とみずほ銀行の相関係数を求めています。(0.66)
ちなみに相関係数0.66となると、完全に一致はしないが、ある程度同じような値動きをする関係になります。
共分散を求める
ここからがポートフォリオ作成のキモになります。
まず3銘柄(A,B,C)にWA,WB,WCの比率で分散投資した際の、ポートフォリオのリスク(σP)の計算式は下記となります。
特にこの式のρσσを、共分散(covariance)と言います。
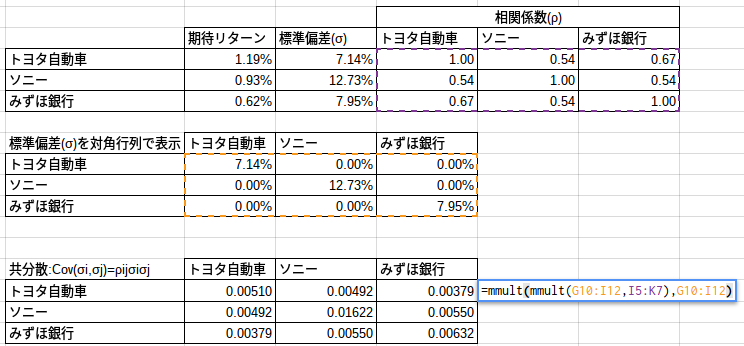
この共分散を計算するステップとして、先ほど求めた標準偏差を対角行列の形に表します。
(図のオレンジ枠部)
この対角行列と、同じく先ほど求めた相関係数を、行列関数(=MMULT)を使い、共分散の式を作成します。
行列関数のため、トヨタ自動車の位置に共分散の計算式を入力すると、他の計算結果も同時に得られます。
ポートフォリオのリターンを求める
ここまでくると、ポートフォリオのリターン/リスク分析は出来たも同然です。
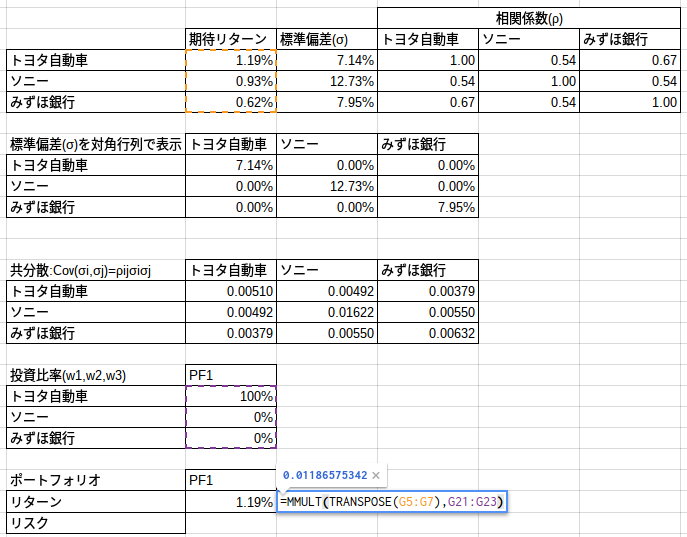
まず、投資比率に応じたポートフォリオのリターンを求めます。
ポートフォリオ1(PF1)では、トヨタ自動車株100%、ソニー0%、みずほ銀行0%に投資をするとします。
株式リターンは単純平均となるので、
(トヨタリターン)✕(投資比率)+(ソニーリターン)✕(投資比率)+(みずほリターン)(投資比率)
=1.19%✕1+0.93%✕0+0.62✕0
=1.19%
が得られます。
これも先ほどと同様に、行列関数(=MMULT)を使い、各銘柄のリターンと投資比率を掛けあわせます。
(ここでは=transposeという、行と列を入れ替える関数を使い、行列計算を行えるようにしています。)
ポートフォリオのリスクを求める
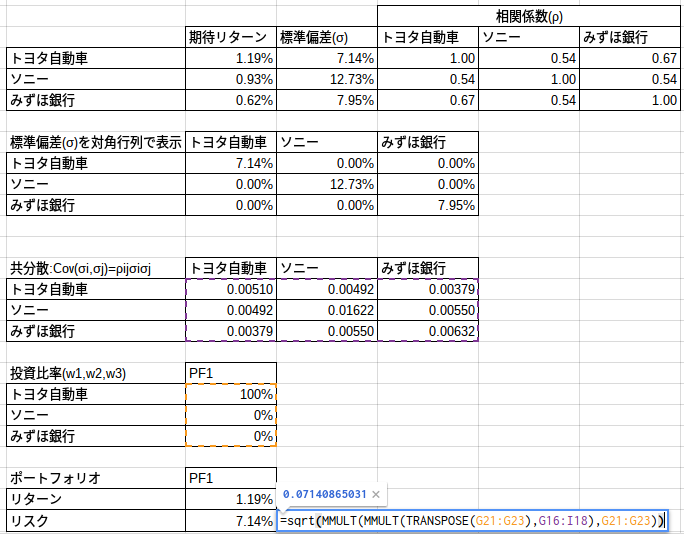
最後にポートフォリオのリスクを求めます。
すでに共分散については求めているため、投資比率を行列関数を使い掛け合わせることで、リスクを求めていきます。
先ほどの3銘柄分散時の計算式は2乗されている点に注意し、平方根を忘れずに計算しましょう。
平方根は=sqrtという関数で計算できます。
今回は10%毎にそれぞれの投資比率を変更し、PF66まで作成しました。
これらを縦軸リターン、横軸リスクでプロットしたものが、最初に紹介したポートフォリオとなります。
行列関数を使えば投資対象が100銘柄でも楽に計算できるので、是非マスターしたいところですね。
kazuの金融講座でも教えているので、興味があればご連絡下さい!
2016年1月追記:銘柄レコメンドシステムについて相談受けました!
最後までご覧頂きありがとうございました
このブログを書いているのはこんな人です。良かったらプロフィールをご覧くださいね。
会社員投資ブログは【こちら】
最新情報もSNSで配信中!
ブログ以外でも、
やっています。フォロー頂けると、最新情報やブログ非公開の話、オフ会情報などを受け取れます。ありがとうございました。
最新情報をお届けします
Twitter でkazuをフォローしよう!
Follow @25_500com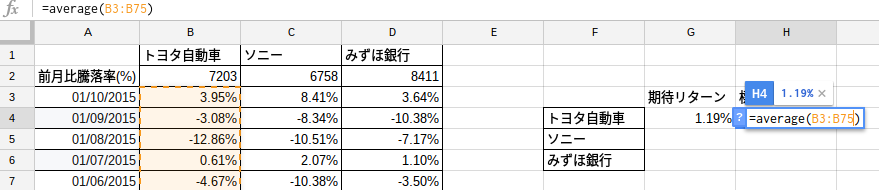








初めてコメントさせていただきます。
今iFree 8資産バランスとi Free NYダウ・インデックスのみの
ポートフォリオで、この記事のようにリスクを計算しようと思ってる
のですが、i Freeシリーズは半年前に登場したばっかで5年間の前月騰落率
を出そうにもデータがないんですが
この場合は、その商品がベンチマークにしているTOPIXだとか
ダウ平均株価とかで5年間の前月騰落率を出して、そこから共分散を出したりして、ポートフォリオのリスクを算出したほうが良いのでしょうか。
くりやまさん
iFreeはいずれもインデックスファンドなので、おっしゃる通りベンチマークとなっている原資産で計算した方が精度いいと思います。
アクティブファンドはある程度投資期間が経ったものを、ポートフォリオに組み入れるべきですけどね。(ファンドマネジャーの手腕が影響大きくなるため)
コメントありがとうございます!
御丁寧な回答ありがとうございます。参考になりました^ ^
すみません。
iFree8資産バランスのデータは
e-maxis 8資産バランスで代用して良いと思いますか?
iFreeの先進国債券でベンチマークにしてる指数の
シティ世界国債インデックスのデータがなく(これだけではないですが)
この指数をベンチマークにしてる指数で乖離率の低い商品を探しましたが
どうも見つからずです^^;
MSCIをベースにしているe-maxisと、様々なベンチマークを使用しているiFreeでは微妙に投資対象が違うので、正確にやるなら代用はしない方がベターですね。。
World Government Bond Index (WGBI)
https://www.yieldbook.com/m/indices/single.shtml?ticker=WGBI
など海外サイトから探せばありそうです。
まあインデックス投資ですし、大まかな資産クラスが合っていれば誤差と範囲かもしれませんね。
ベンチマークが一つ違うだけで
値動きもそんな違ってくるものですかね。
iFreeとe-maxis
大まかな資産クラスが合っていれば誤差の範囲だと思いますよ。
はじめまして。機会係数曲線を調べていて、こちらを参考にさせていただきました。
投資信託の配分比率を検討するため、上記計算式をExcelで使っています。
私自身は、投資経験3ヶ月です。(国内株現物とネット証券のオープン投信のみ)
質問です。間違っていたら申し訳ないのですが、
相関係数ρに負の値が存在する場合、共分散が負になる部分があり、
SQRTの引数が負になってエラーになることがあります。
この場合、どうやってリスクのポートフォリオを求めればいいでしょうか。
ヌリイカさん
こんばんは。
kazuです。
ポートフォリオのリスクを求める際の計算式が間違っていると思われます。
相関係数も共分散も、負になる場合はありますが、そのままSQRTすることはありません。
SQRTする対象はσ(シグマ)の二乗のため、必ず0以上となっています。
MMULTの位置によっても計算式が変わるので、一度見直して見てください。
コメントありがとうございます!
kazuさま
レスありがとうございました。
相関係数ρのとりうる値は、-1<ρ<-1ですよね。
計算方法はρ×σ×σなので、ρ<0の場合は負になります。
その負になる所が、たまたま投資比率が高い(90%以上)場合に、SQRTの中が負になるのです。
極端な投資比率が原因なのでしょうか。こういうケースは考慮しない方がよいということかなと、思っています。
すみませんがアドバイスをお願いいたします。
ヌリイカさん
返信ありがとうございます。
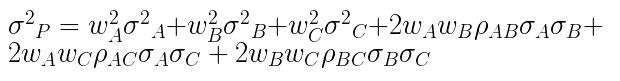
下記計算式に、銘柄A、B、Cの標準偏差、それぞれの共分散、投資比率を代入してみてください。
負にならないと思います。(そもそもポートフォリオの標準偏差σを二乗しているので、必ず0以上になります。)
また下記図は極端な例として、トヨタとみずほ銀行の相関係数が-1.0(完全な逆相関)だったときのポートフォリオを作ってみました。

分散図で一番左側にある点が最もリスクが低く、このときの投資比率はトヨタ:ソニー:みずほ銀行=50:0:50でした。
このケースでも、σの二乗は負になることなく、もちろんSQRT後もエラーになりません。
参考になれば幸いです。
よろしくお願いします。
kazuさま
たびたびすみません。以下のケースを見てください。
相関係数ρ12=-1, ρ13=0, ρ23=-1
分散σ1=0.2, σ2=0.1, σ3=0.2
→(ρijσiσj)={0.04, -0.02, 0.00,
-0.02, 0.01, -0.02,
0.00, -0.02, 0.04}
※ ρは1回、σは2回掛けるので、ρσσが負になることがあります。
配分率 r1=20%, r2=60%, r3=20% とすると、SQRTの引数が負になります。
ヌリイカさん
面白い問題、ありがとうございます。
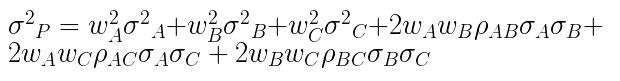
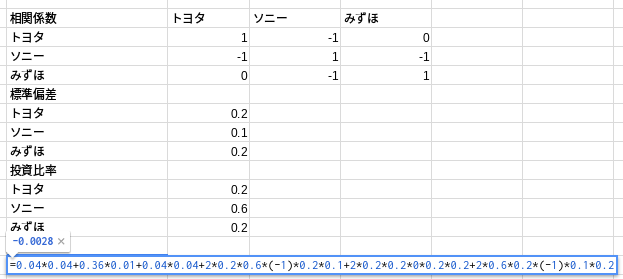
ブログでも紹介している公式に当てはめると、
相関係数:ρAB=-1、ρAC=0、ρBC=-1、(分散σ^2ではなく)標準偏差:σA=0.2、σB=0.1、σC=0.2、投資比率:WA=0.2、WB=0.6、WC=0.2となります。
このポートフォリオのリスクは、
=0.04*0.04+0.36*0.01+0.04*0.04+2*0.2*0.6*(-1)*0.2*0.1+2*0.2*0.2*0*0.2*0.2+2*0.6*0.2*(-1)*0.1*0.2
=-0.0028
となり、確かにマイナスになりました。
ええっ!なんで!と一瞬戸惑ったのですが、相関係数があり得ない値になっています。
AとBが完全な逆相関(ρAB=-1)、BとCが完全な逆相関(ρBC=-1)の関係のとき、AとCは完全な相関(ρAC=1)関係になります。
=0.04*0.04+0.36*0.01+0.04*0.04+2*0.2*0.6*(-1)*0.2*0.1+2*0.2*0.2*1*0.2*0.2+2*0.6*0.2*(-1)*0.1*0.2
=0.0004
となり、正の値になります。
これを平方根(SQRT)した0.02が、ポートフォリオのリスクになります。
kazuさま
コメントありがとうございました。ありえない係数だったのですね。
実はこのページを見つけた初日に、自分で投信10銘柄のポートフォリオを
組んでみて、配分率15通りのうち1つで、リスクが「#NUM!」となって
びっくりしたため、今回の質問をさせていただきました。
その時のデータは、保存していなかったので、似たようなケースができないか
試行錯誤した結果見つけたのが、前回の私の数値です。
10銘柄で何通りも試していたので、どこかの計算式が間違っていたのだろう
と思います。
今回、親切に説明してくださって、ありがとうございました。
kazuさん
始めまして。私は、高校生です。最近、株式投資に興味があり、サイトをめぐっている内に、こちらのブログにたどり着きました。大変面白い記事だったので、実際に無作為に選んだ11銘柄で、Excel(Microsoft)でやってみました!
投資比率を、10%と5%に分けてPF55通りまで作り、ポートフォリオのリターンとリスクまでは、ブログの様に算出することが出来ました。しかし、55通りの中で、どれか一番最適な投資かを決めたいと考えているのですが、この場合どのようにすればよろしいのでしょうか?
私の場合、最後に算出したポートフォリオの(リターン-リスク)が最大になるものが一番期待値が高いと考えていましたが、これが正しいのかどうかもわかりません。
余りにも、無知で申し訳ございませんが、よろしければ、教えて下さると幸いです。
PS.株式投資について、おすすめの本も教えて頂けると幸いです。
mikaさん
コメントありがとうございます。
一般的には、リターン÷リスクで計算される、シャープレシオが大きいものが最適な投資になります。
x軸にリスク、y軸にリターンを持っていることを考えると、シャープレシオはそのポートフォリオにおける傾きにあたります。
傾きが大きいものほど、少ないリスクで高いリターンを上げられるポートフォリオとなるわけです。
オススメの本ですが、
初心者向け http://amzn.to/2i9d35d
株式市場の裏 http://amzn.to/2jrCagy
オプション取引 http://amzn.to/2ABypjC
高校生でこの記事に行き着くのは、かなりポテンシャル高いと思うので、ちょっと難しめの本も紹介しました。
コメントありがとうございます!
mikaさま
参考までに私が以前作ったグラフです(X:リスク Y:リターン)
http://25-500.com/wp/wp-content/uploads/2017/11/185133.png
原点(0,0)から各ポートフォリオへの直線の傾きが最大のものが、
リスクに対するリターンが優れていることになります。
私は、以下の書籍で「機会曲線」に興味を持って、こちらのサイトにたどり着きました。社会人向けですが、高校生の学力でも大丈夫だと思います。よかったらお読みください。
http://www.kadokawa.co.jp/product/321612000501/
kazuさま
各URLがまずかったら削除をお願いします。
ヌリイカさん
こんばんは。
補足ありがとうございます。
外部リンクはSEO的に減らしたいので、画像をコピーさせてもらいました。
オススメの本も、面白いですよね。
コメントありがとうございます!
kazuさん ぬりいかさん
ありがとうございました!シャープ・レシオについて簡単に勉強しました。
リターン-リスクではなく、リターン÷リスクでしたね。わかりやすく教えて頂きありがとうございます。
本についても、本屋さんで読んでみます!
丁寧に教えて頂き、ありがとうございました。
kazuさん
はじめまして、勉強させていただいています。
10銘柄のポートフォリオを作成したいと思い
投資比率の表を投資配分(10%単位)で作成したいのですが
楽に作成する方法はございますでしょうか。
手で入力していると気が狂いそうです^^;
よろしくお願いいたします。
さぼてんさん
コメントありがとうございます。
3銘柄なら手入力(オートフィル)でもいいと思いますが、それ以上ならVBAのfor next文で書くと思います。
kazuさん
アドバイスありがとうございます。
やってみます!